Eclairage scientifique
Propagation du SARS-CoV-2 et aération d'une pièce
Le contexte
Imaginons une classe de lycéens, dont un des élèves, sans le savoir, est porteur du SARS-CoV-2, le coronavirus responsable de la Covid-19. Peu symptomatique et pas encore diagnostiqué, l'élève reste quelques jours en cours tout en étant contagieux.
Ce que l'on sait
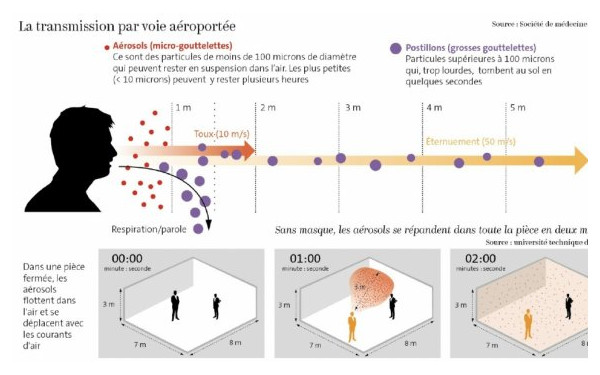
Document n°1 - « Le rôle des aérosols dans les contaminations a été trop longtemps négligé » - Crédit : Antoine Flahault épidémiologiste et directeur de l’Institut de santé globale (ISG) à l’université de Genève, en Suisse.
À ce jour, on pense que le mode de transmission majeur voire dominant du virus, est la transmission par voie aérienne.
Quand on tousse, mais aussi quand on parle, postillonne et même simplement par notre respiration, nous émettons tout un ensemble de gouttelettes, dont la taille peut aller d’une centaine de microns à moins d’un micron. Ces gouttelettes proviennent de notre salive, des muqueuses des poumons et des voies respiratoires.
Même si vous n’avez pas de symptômes comme la toux ou les éternuements, vous allez naturellement émettre ces gouttelettes.
Or, contrairement à de grosses gouttelettes, les petites gouttelettes peuvent rester en suspension dans l’air. Les mouvements d’air ambiants sont suffisants pour compenser leur chute sous l’effet de la gravité.
Pour ces micro-gouttelettes en suspension dans l’air, on utilise le terme d’aérosols. Ces aérosols en suspension peuvent diffuser librement dans une pièce close, et venir contaminer une personne, même si elle se situe à plus de deux mètres du porteur du virus.
Il n’existe évidemment pas de frontière stricte entre les grosses gouttelettes dont on a parlé, et les aérosols. Plus les gouttelettes sont grosses, plus elles vont tomber rapidement au sol, plus elles sont petites, plus elles sont susceptibles de rester en suspension. (Voir le document n°1)
Depuis maintenant plusieurs mois, les preuves s’accumulent quant à l’importance de ce mode de contamination, qui avait été initialement sous-estimé.
Ce que l'on recherche
D'une part |→ Combien de camarades va contaminer un élève porteur du virus, dans sa salle de classe ?
D'autre part |→ Comment faire pour que si possible cela ne soit aucun ? (à défaut, limiter au mieux le mode de transmission)
Ressources mises à disposition
Données
- Lors de la ventilation pulmonaire, on rejette environ 0,5 m3 d’air par heure. Si on parle beaucoup ou qu’on chante, alors les valeurs seront plus élevées, jusqu’à 1 m3 d’air rejeté par heure.
- Dans 1 m3 d'air expiré, on estime qu'il existe jusqu'à 1000 copies du virus.
- Les copies de virus sont contenues dans des micro-gouttelettes encore appelées aérosols.
- Un masque chirurgical a une efficacité d’environ 90%.
- Si le masque n'est pas porté de façon parfaite alors cela augmente de 5% la fraction de virus qui s'échappent.
- La salle de classe fait 50 m2 et possède 3 m de hauteur sous plafond.
- L'air de la pièce est totalement renouvelé en deux heures.
- Le nombre (N) d'élèves dans la classe est de 30.
- La probabilité (p) d'infection par un virus est estimé à 10%.
- La fraction (k) d'air expiré contient environ 4% de CO2.
Définitions
- Volume d'air (V) = gaz occupés dans un espace donné. [en m3]
- Débit d'air expiré (Q) = volume d'air expiré par unité de temps. [en m3.h-1 ou m3/h]
- Concentration en virus (Cv) = nombre de copies du virus par unité de volume. [en virus.m3 ou virus/m3]
- Fraction de virus qui s'échappent (f) = pourcentage de virus franchissant un masque et/ou sortant du nez non couvert. [en %]
- Taux de renouvellement de l'air (λ) = nombre (n) de fois où l’air de la pièce est renouvelé à chaque heure. [en n.h-1 ou n/h]
- Temps d’exposition au virus (𝛕) = nombre d'heures où un sujet sain est exposé au virus ambiant, suite à la présence d'un élève contagieux. [en h]
- Probabilité de contamination (p) = risque d'infection à chaque virus [en %]
- Concentration en quantum d’infection (Cq) = « dose » de virus dans un volume d'air expiré [en virus.m3 ou virus/m3]
- Surplus de CO2 à l'équilibre dans une pièce (Δ) = taux de CO2 ajouté en plus du taux de base de l’air extérieur [en %]
- Seuil de tolérance (ε) = risque admissible [en %]
Stratégie suivie
Pour répondre aux deux questions, c'est à partir de connaissances physiologiques et de principes physiques simples qu'on se propose de faire des calculs. Des formules mises à disposition seront utilisées afin d'établir un modèle mathématique et des ordres de grandeur importants.
Étapes de la mise en œuvre du raisonnement
Première étape : calcul de la quantité de virus rejetés dans l’air ambiant par l'élève porteur, à chaque heure, dans la salle de classe dont l'air est renouvelé.
Deuxième étape : calcul du nombre d'infections que cela peut causer, en considérant que l’élève contagieux reste 3 jours en classe avant d’être testé et isolé, à raison de 7h de cours par jour.
Troisième étape : réflexion menée sur la façon de réduire le risque de transmission du virus au sein d'une salle de classe.
Démarche suivie
Première étape du raisonnement
En respirant, l'élève infecté rejette environ 0,5 m3 d’air par heure. S’il parle beaucoup ou qu’il chante, alors les valeurs seront plus élevées, jusqu’à 1 m3 d’air rejeté par heure.
On note Q ce débit d’air expiré, en unité de volume par unité de temps.
A ce stade recherchons combien y-a-t-il de virus dans cet air expiré ?
La réponse immédiate est assez difficile. En première approximation, admettons qu’il puisse y avoir 1000 copies du virus par m3 d’air expiré. (Nous reviendrons un peu plus loin sur cette valeur)
Ayons en mémoire que ces copies du virus ne sont pas à l’air libre, mais contenues dans des micro-gouttelettes encore appelées aérosols.
Supposons seulement que tous les aérosols contenus dans 1 m3 d’air expiré correspondent à 1000 exemplaires du virus.
On note Cv, la concentration en virus dans un volume d'air expiré.
Considérons le port du masque.
S’il est bien mis, alors il absorbe une bonne partie des gouttelettes, et par conséquent une bonne partie des exemplaires du virus.
Un masque chirurgical a une efficacité d’environ 90%. Autrement dit, ce ne sont que 10% des virus qui passent au travers.
On note f cette fraction de 10% soit 0,1.
Deux remarques
- On considère un masque et non une visière. En effet, même si une visière peut capturer les grosses gouttelettes qui sont projetées quand on éternue, elle ne permet pas d'arrêter les aérosols en suspension.
- Le masque doit être bien porté, y compris sur le nez. On parle de gouttelettes contenues dans la respiration qui s'effectue beaucoup par le nez. Si le masque est sous le nez alors tout cet air contaminé sort sans difficulté.
Malheureusement pour nos élèves, le masque n’est pas tout le temps porté de façon parfaite. Au total, on estime que ce sont 15% des virus qui passent. Soit une fraction f = 0,15.

Document n°2 - Les calculs de la première étape du raisonnement.
Faisons le produit des trois quantités : le débit d'air expiré (Q) par la concentration en virus dans l'air expiré (Cv) par la fraction (f) de virus qui échappe au masque.
On a Q x Cv x f
Avec Q = 0,5 m3 / h
Cv = 1000 virus / m3
f = 0,15
Soit 0,5 x 1000 x 0,15 = 75 virus / h
On obtient ainsi la quantité de virus rejetés dans l’air ambiant par l'élève porteur, à chaque heure ; c'est-à-dire 75 virus expirés par heure.
Ensuite on doit tenir compte du fait que les micro-gouttelettes qui contiennent les virus, une fois rejetées, diffusent assez vite dans toute la salle de classe. Par conséquent, les 75 virus expirés par heure se retrouvent dilués dans l’ensemble du volume de la pièce.
Si la salle de classe fait 50 m2 et qu'elle possède 3 m de hauteur sous plafond, alors ces 75 virus seront dilués dans un volume V de 150 m3 d’air.
Donc la concentration moyenne une fois les virus dilués est de 75 divisé par 150, soit 0,5 virus par m3.
Cela peut paraître peu. Sauf que souvenez-vous, cette concentration moyenne de 0,5 virus par m3 est ajoutée dans l’air à chaque heure.
En théorie, la concentration en virus dans l’air ambiant devrait augmenter en continu : 0,5 puis 1 puis 1,5 puis 2 etc. heure après heure.
Ce raisonnement serait correct en considérant la salle de classe comme un « bocal » parfaitement étanche. Heureusement pour les personnes présentes l'intérieur, une pièce n’est jamais étanche. Il y a des bouches d’aérations ou peut-être même une ventilation mécanique qui extrait l’air et le rejette à l’extérieur. Ou encore probablement qu’on aère de temps en temps en ouvrant les fenêtres.
Il y a plusieurs moyens de quantifier tous ces phénomènes.
Une façon simple, est de suivre le taux de renouvellement de l’air de la pièce |→ Combien de fois l’air de la pièce est-il renouvelé à chaque heure ?
Supposons qu’il faille deux heures pour tout renouveler. Cela veut dire que le taux de renouvellement est de 0,5 fois par heure.
On note lambda (λ) le taux de renouvellement de la pièce.
Cela veut dire qu'à chaque heure, les virus rejetés ne se diluent pas dans un volume (V) d'air frais de 150 m3, mais dans 0,5 fois cette valeur.
En faisant bien le calcul, on peut montrer qu’entre ce qui est rejeté par l'élève porteur et ce qui est renouvelé, la concentration de virus dans l’air ambiant va atteindre un équilibre égal à (Q x f x Cv) divisé par (λ x V).
(Q x f x Cv) / (λ x V)
Avec les chiffres qu’on a choisi, l'application numérique est :
(0,5 x 0,15 x 1000) / (0,5 x 150) = 1 virus / m3
Le résultat est de 1 virus par m3.
|→ Est-ce que c’est beaucoup 1 virus par m3 ?
Deuxième étape du raisonnement
On recherche désormais à estimer |→ combien d’infections le rejet d'un virus par m3 peut-il causer ?
Mettons-nous à la place d’un autre élève situé ailleurs dans la classe.
Ce dernier respire aussi l’air ambiant. Il inspire et expire au même rythme que ce qu’on a supposé tout à l’heure soit un taux Q de 0,5 m3/h.
Si l’élève contagieux reste 3 jours en classe avant d’être testé et isolé, alors à raison de 7h de cours par jour, l'élève sain est exposé au virus ambiant pendant une vingtaine d’heures au total (en sous estimation).
On note tau (𝛕) ce temps d’exposition.
𝛕 = 20 h
On note Q𝛕 le volume d'air inhalé
Q𝛕 = Q x 𝛕
Q𝛕 = 0,5 x 20 = 10 m3
D'où 10 m3 d’air inhalé en une heure par un élève exposé au virus ambiant.
Si on multiplie cette valeur par la concentration en virus dans l’air ambiant, alors il y a un virus par m3 multiplié par 10m3/h.
Cela fait 10 exemplaires du virus inhalés par un élève sain sur les 3 jours d’exposition.
Sauf qu’on a oublié le masque !
Le masque filtre 90% des virus entrants, donc seulement un seul sur les 10 va passer, ça ne fait plus qu’un seul virus inhalé.

Document n°3 - Calculs de la deuxième étape du raisonnement.
Le nombre de virus inhalés au total se calcule selon la formule :
(𝛕 x Q2 x f2 x Cv) / (λ x V)
[20 x (0,5 x 0,5) x (0,1 x 0,1) x 100] / (0,5 x 10) = 1 virus inhalé
Un seul virus inhalé : est-ce que c’est grave ? - Est-ce que ça suffit à contracter la Covid-19 ?
Eh bien probablement pas !
A chaque virus, il y a une certaine probabilité « p » qu’il infecte vraiment un individu. Combien vaut cette probabilité ?
On l'estime à 10% : seulement un risque sur 10 à chaque exemplaire du virus. (On en rediscutera plus loin)
On multiplie alors la formule précédente par p.
(𝛕 x Q2 x f2 x Cv x p) / (λ x V)
Cela donne la probabilité d’être infecté égale à 10%
Le pauvre élève qui a inhalé en moyenne 1 virus au cours de ses 20 heures d’exposition, n’a que 10% de chance (ou de risque) de tomber malade.
Franchement ça va ! - Ça va, sauf que les élèves sont 30 dans la classe, à être tout autant exposés à ce mode de contamination.
En conséquence, si chaque élève à 10% de chance de tomber malade, on est à peu près certains de récupérer un, voire plusieurs cas.
Pour simplifier, on peut multiplier la formule par N, le nombre de personnes présentes.
(N x 𝛕 x Q2 x f2 x Cv x p) / (λ x V)
Cette formule donne la probabilité qu’il y ait une transmission du virus.
Rappelons que même s’il n’y a qu’une transmission, en fait c’est beaucoup.
Si chaque malade transmet le virus à plus d’une personne, alors le nombre de reproduction, le fameux « R0 » est supérieur à 1.
Dans ce cas, l’épidémie continue de façon exponentielle.
Ce que l'on veut
Amener la transmission en-dessous de 1. On veut en moyenne moins d’une transmission par malade.
Et comme ici on raisonne juste sur le temps passé en classe, on aimerait bien amener ce chiffre vraiment en dessous de 1.
Observons ensemble la formule obtenue. Quels renseignements nous apporte-t-elle ?
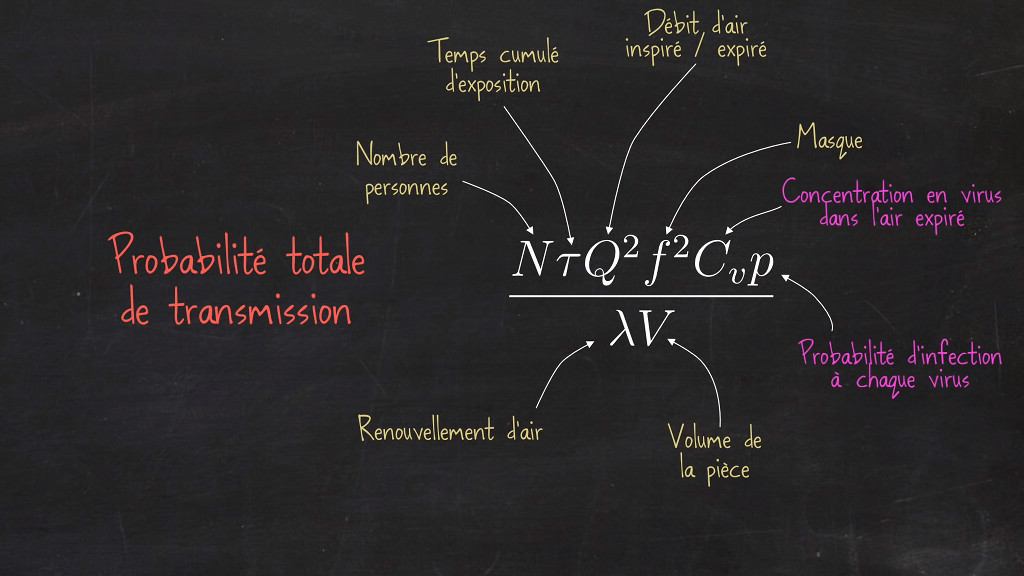
Document n°4 - Les renseignements apportés par la formule obtenue lors de la deuxième étape du raisonnement.
Elle nous dit des choses intéressantes sur la transmission par voie d’aérosols.
Premièrement, c’est proportionnel au temps d’exposition cumulé tau (𝛕) [C’est assez logique, si on reste deux fois plus longtemps, le risque double.]
Deuxièmement, le coefficient de filtration f apparait au carré [Il y a un double effet des masques qui limitent les virus expirés par le porteur, et ceux inhalés par le receveur. Un masque bien porté, c’est seulement 10% de virus qui passent à chaque fois. Cela réduit au total la transmission d’un facteur 100. L’effet du masque est énorme.]
Troisièmement, au dénominateur, on voit qu’on a le volume (V) de la pièce et le taux de renouvellement de l’air (λ). [Plus la pièce est grande et plus l’air est renouvelé, moins on prend de risques. C’est logique, mais c’est bien de le voir.]
Et puis, ici il reste deux termes dont je vous ai promis qu’on reviendrait dessus : d'une part la concentration en virus dans l’air expiré (Cv), et d'autre part la probabilité (p) de contamination quand on inhale une copie du virus.
Les valeurs qui ont été fournies sont crédibles, mais sur lesquelles on a en fait une grande incertitude.
Retour sur les incertitudes de Cv et de p
C’est assez difficile de connaître leurs valeurs. Pour autant, toute cette analyse se trouve-t-elle discréditée ?
Eh bien non, car en fait ce qui compte, c’est le produit de ces deux quantités : 1000 virus par m3 expiré soit Cv la concentration en virus dans l'air expiré, et 10% soit la probabilité p de contamination (ou d'infection à chaque virus). C’est la même chose que 10 000 virus par m3 et 1% de probabilité.
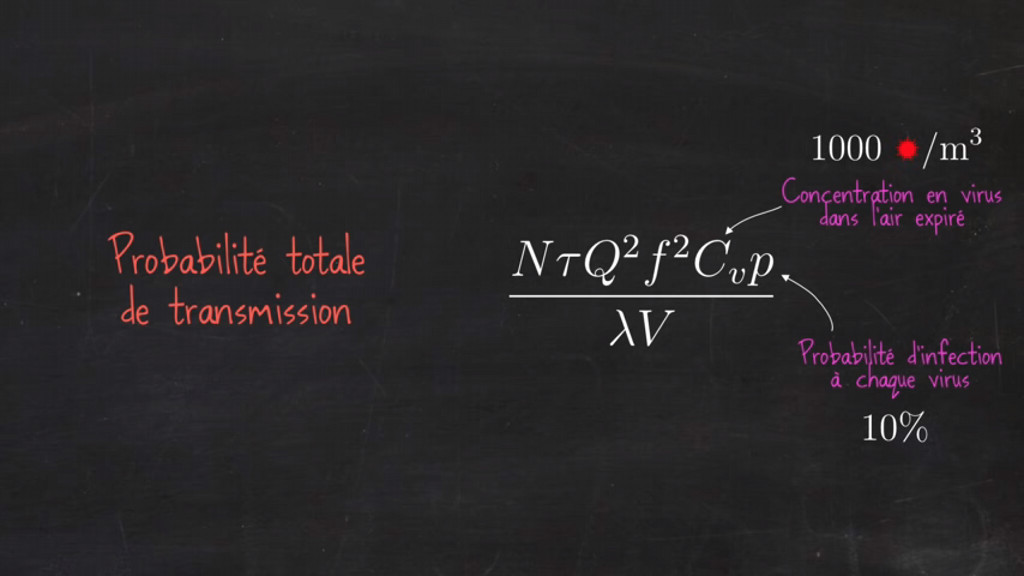
Document n°5 - Probabilité totale de transmission : exemple 1.
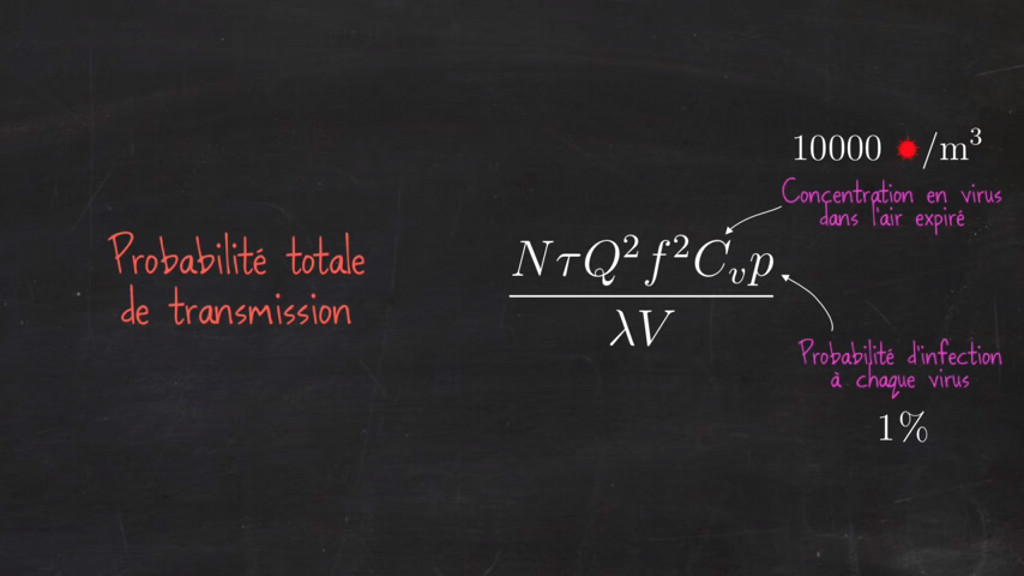
Document n°6 - Probabilité totale de transmission : exemple 2.
Imaginez que cette probabilité soit 10%. Dans ce cas, cela veut dire qu’il faut en moyenne une exposition à 10 copies du virus pour être contaminé.
1000 virus par m3, c’est 100 fois cette quantité ou « dose ». On appelle cette « dose » un quantum d’infection.

Document n°7 - Un quantum d’infection.
Ce « quantum » n'a rien à voir avec la mécanique quantique. Il s'agit juste de la quantité « typique » qu’il faut pour être infecté.
Ainsi, 1 000 virus par m3, représentent donc 100 quantum d’infection par m3.
Et si cela avait été 10 000 virus avec une probabilité de 1%, cela aurait été la même chose. Cela aurait fait aussi 100 quantum d’infection par m3.
Dans notre analyse, on oublie la concentration en virus (Cv) et la probabilité (p) d’infection. On remplace le produit des deux (Cv x p), par la concentration en quantum d’infection dans l'air expiré que l'on note Cq.
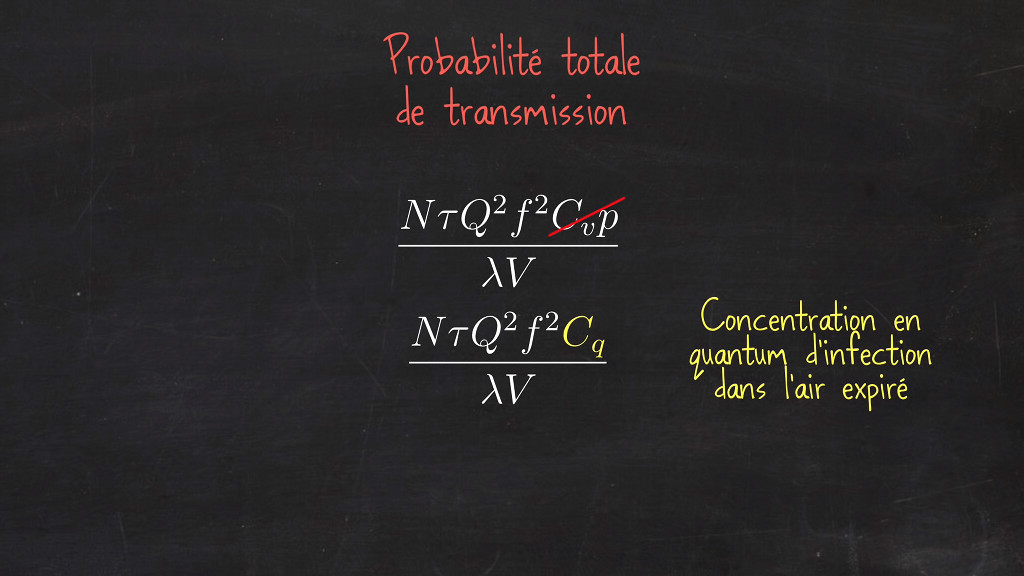
Document n°8 - Devenir de la la formule en remplaçant le produit (Cv x p), par la concentration en quantum d’infection dans l'air expiré que l'on note Cq.
La formule devient :
(N x 𝛕 x Q2 x f2 x Cq) / (λ x V)
|→ Pourquoi est-ce mieux ainsi ? - Parce que c’est quelque chose que l'on peut plus facilement estimer.
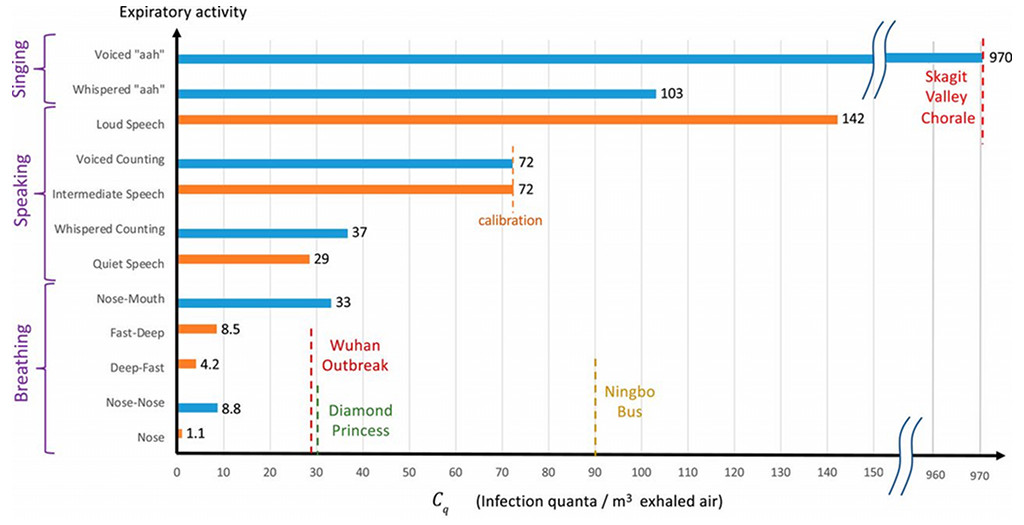
Document n°9 - Estimation d'un quantum d'infection selon un événement de contamination.
Martin Bazant et John Bush sont deux physiciens qui ont écrit un article scientifique dans lequel ils ont pris les données de divers événements de contamination. Ils ont pu estimer des valeurs moyennes pour la concentration en quantum d’infection émis par un malade.
Pour une activité normale, la valeur typique qu’ils ont obtenu est d’environ 70 quantum par m3 d’air expiré.
Toutefois, dans le cas d'une chorale, où les gens chantaient, la valeur serait plus proche de 900 quantum par m3 d’air expiré.
On imagine volontiers que lorsqu'on chante fort, on expulse plus de gouttelettes qui viennent peut-être de régions différentes des poumons, et que cela fasse augmenter de beaucoup la concentration en quantum d’infection de l’air expiré.
Évidemment cette estimation va dépendre de tout un tas de facteurs : l’état de symptôme du malade, la population cible et aussi bien sûr, la souche du virus.
Si certains variants, comme le fameux variant alpha (anglais) ou encore le fameux variant delta (indien) sont plus contagieux, alors cela va se traduire par des concentrations en quantum plus élevées.
Notez qu’on ne sait pas forcément si avec les variants les gouttelettes d’aérosol sont plus concentrées en virus, ou bien si c’est la probabilité d’infection associée à un exemplaire du virus qui est plus élevée.
Mais l’effet sur la concentration en quantum d’infection est le même : cela va l’augmenter peut-être de 50%.
Dans tous les cas, vous voyez qu'initialement la valeur choisie de 100 quantum par m3 était assez raisonnable. On n’a pas de valeur très précise à ce sujet, mais c’est essentiellement le seul paramètre de l’analyse sur lequel on ait une incertitude.
En prenant une bonne marge de sécurité, cette réflexion sur le quantum d’infection peut nous permettre d’avancer dans le raisonnement.
Troisième étape du raisonnement
Revenons à la formule établie précédemment.
On s'est fixé de limiter la reproduction du virus, et faire descendre cette valeur assez en dessous de 1.
Pour être large avec nos incertitudes, on va dire qu’on se fixe un seuil de tolérance à 10%. On note ce seuil epsilon (ε).
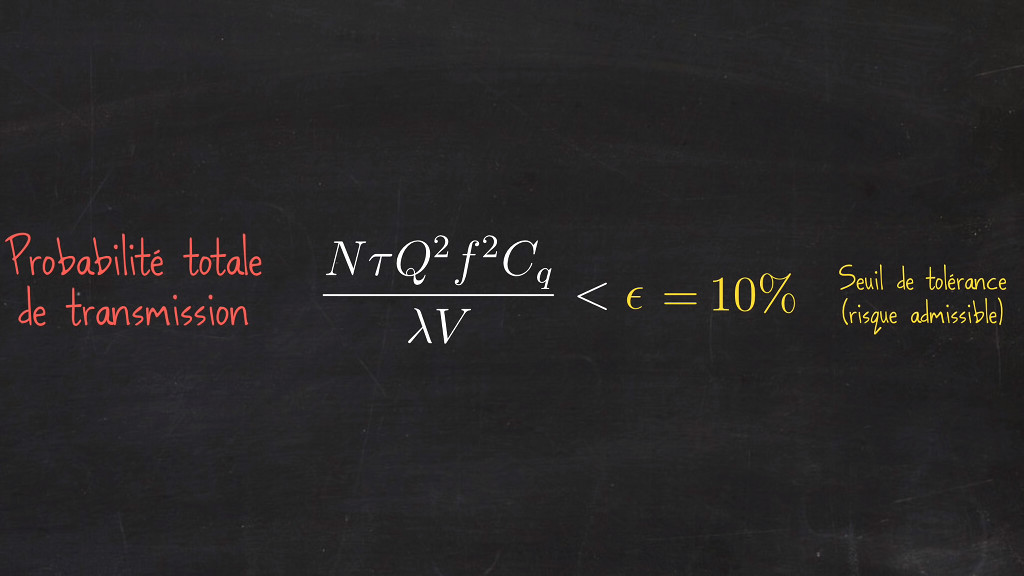
Document n°10 - Seuil de tolérance.
Ce qu’on veut :
(N x 𝛕 x Q2 x f2 x Cq) / (λ x V) < ε = 10% Soit le seuil de tolérance (risque admissible)
|→ Que peut-on faire pour respecter ce seuil ?
On peut se poser la question pour chaque situation où on réunit des personnes dans une même pièce.
Prenons les caractéristiques fournies pour la salle de classe.
Premièrement on peut limiter le nombre de personnes présentes N et le temps d’exposition tau (𝛕). De ce point de vue, la pratique de la demi-jauge va évidemment dans le bon sens.
Autre chose essentielle, il faut bien porter le masque.
Rappelons que le facteur f a un effet au carré.
Aussi, il faut aussi éviter les activités comme le chant ou le sport qui augmentent le débit de respiration Q.
Pour le sport cela peut faire un facteur 10 sur le débit Q. Mis au carré cela fait un facteur 100.
Donc le sport en intérieur et pire, sans masque, c’est non !
Le volume (V) de la pièce, a priori ne peut pas trop être changé.
Il reste lambda (λ), le taux de renouvellement de l’air.
L'exemple choisi au départ est assez pessimiste, puisque qu'un renouvellement toutes les 2 heures conduit à considérer λ = 0,5 fois par heure.
C’est une valeur typique pour des locaux résidentiels, mais en local collectif, avec un bon système de ventilation ou une aération périodique, on peut faire beaucoup mieux.
On peut multiplier cette valeur par 5 voire 10, et donc diminuer d’autant le risque.
Si on a la main sur un système de ventilation mécanique, un repère typique est d’imposer un débit de ventilation d’environ 30 m3 par heure et par personne.
Avec une classe de 30 élèves cela fait 900 m3 par heure. Ce qui veut dire que dans une pièce dont le volume est de 150 m3 le renouvellement de l'air se fait 6 fois par heure.
6 fois pour lambda (λ) au lieu de 0,5 cela permet de diminuer le risque d’un facteur 12.
Ce résultat est bien à condition de disposer d'une ventilation mécanique dont on contrôle le débit. Mais, dans beaucoup de situations ce n'est pas le cas.
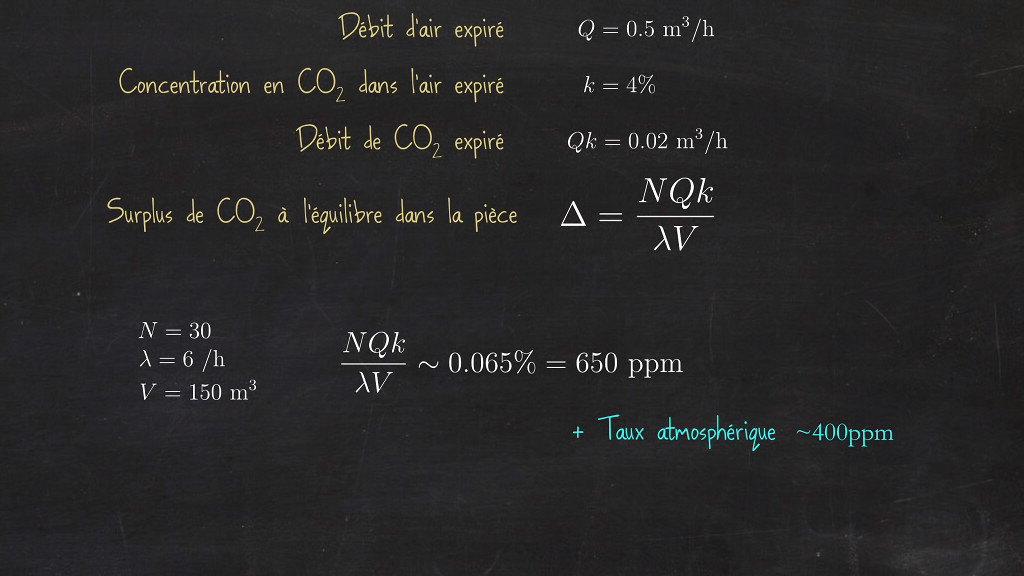
Document n°11 - Prise en compte du dioxyde de carbone (CO2) dans l'air expiré.
Alors comment faire pour estimer lambda (λ) et faire en sorte d’atteindre des valeurs assez hautes ?
Une solution pour traiter ce problème est de mesurer le taux de CO2 dans la salle.
En effet, nous pouvons considérer le CO2 presque comme les virus : on en rejette une quantité à peu près déterminée à chaque heure.
En somme, dans l’hypothèse où il y ait un malade dans la pièce, surveiller la concentration en CO2 nous indique comment évolue la concentration en virus.
Réalisons une approche chiffrée :
- les élèves respirent 0,5 m3 d’air par heure [Débit noté Q] ;
- l’air expiré contient environ 4% de CO2 [Fraction notée k].
La formule Q x k permet de calculer le volume d'air de CO2 émis chaque heure.
0,5 x 0,04 = 0,02 m3/h soit environ 20 L de CO2 émis chaque heure, pour chaque élève.
Comme pour le virus, le CO2 s’accumule et sa concentration augmente, et comme pour le virus, ce taux est dilué par le renouvellement de l’air.
Nous retrouvons le même genre de raisonnement avec à l’équilibre un taux moyen égal à Q x k fois N (le nombre d’élèves), divisé par lambda (λ) x V.
Δ = (N x Q x k) / (λ x V)
Attention ! En réalité ce n’est pas le vrai taux moyen. Il s'agit plutôt de ce qui est ajouté en plus du taux de base de l’air extérieur.
Δ correspond au surplus de CO2 à l'équilibre de la pièce.
S'il y a 30 élèves dans 150 m3, que lambda (λ) est de 6, alors :
Δ = (30 x 0,5 x 0,04) / (6 x 150) = 0,00067 soit 0,067%
Cela fait environ 0.065% de CO2 en plus.
La concentration de CO2 dans l'air est le plus souvent exprimée en ppm, parties par millions et non en %.
Aussi, 0.065% de CO2 correspond à 650ppm, à ajouter au taux de base de l’air extérieur qui est 400ppm. Au total, cela fait un peu plus de 1 000ppm de CO2 dans la pièce.
Avec un taux de renouvellement plus faible, on aurait des valeurs plus élevées.
Cependant, on peut prendre le problème à l’envers : si on souhaite tenir l’objectif de renouvellement de lambda (λ) égal à 6, avec le nombre de 30 élèves et le volume de pièce choisi à 150 m3, alors il faut se fixer pas plus de 1 000ppm de CO2 en moyenne dans la salle de classe.
D'ailleurs, sans avoir peur des formules, on peut combiner l'estimation de surplus de CO2 avec l'objectif fixé sur la probabilité de transmission virale, pour traduire le tout en un objectif sur le surplus de CO2.
Cela donne une élégante formule qui ne dépend plus des caractéristiques de la pièce.
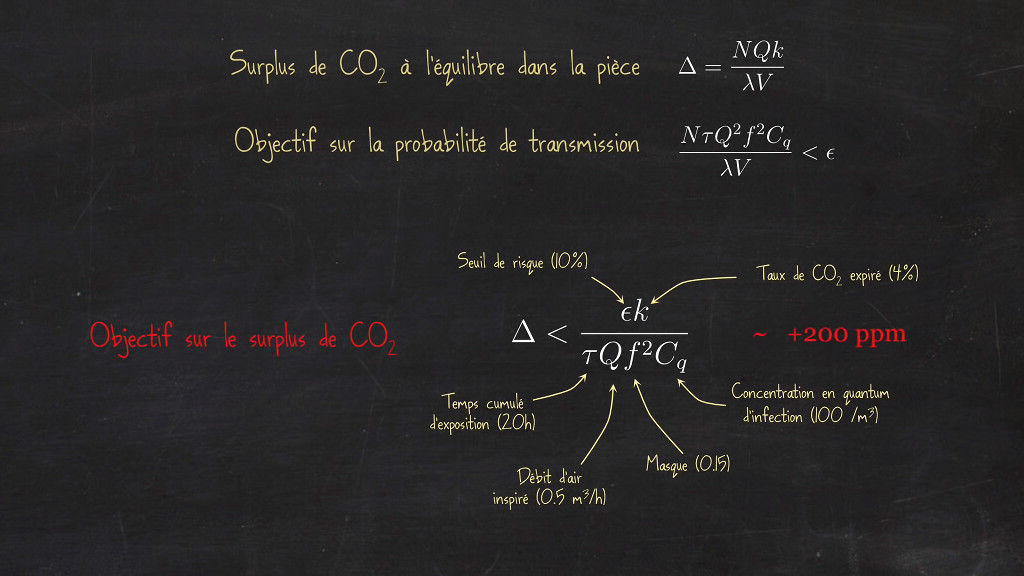
Document n°12 - Objectif sur le surplus de CO2.
Avec des valeurs un peu plus conservatrices on trouve un objectif de surplus de CO2 moyen d'environ 200ppm.
Ajouter les 400ppm de l'atmosphère cela conduit plutôt à un objectif total moyen de 600ppm.
Une façon de le faire, c’est de mesurer le taux de CO2 en direct (grâce à un capteur), et d’ouvrir en grand les fenêtres régulièrement pendant quelques minutes, pour revenir au niveau de base de 400ppm, et osciller comme cela autour de l'objectif fixé.
Dans un article paru dans le numéro de Décembre 2020 de « Pour la science », Jean-Michel Courty, Édouard Kierlik et Benoît Semin ont rapporté des mesures que Jean-Michel Courty a faites dans son bureau, où on voit qu’en quelques minutes d’ouverture des fenêtres, on retombe presque au taux de base. Le temps nécessaire va dépendre du vent, de la géométrie de la pièce, des fenêtres etc.
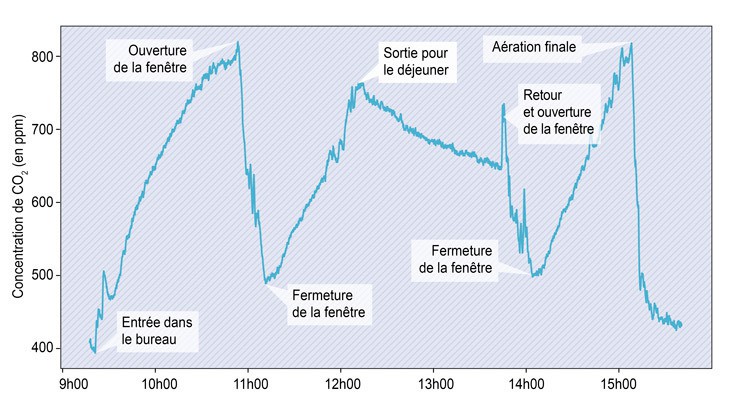
Document n°13 - Variation de la concentration de CO2, en alternant l'ouverture et la fermeture de la fenêtre d'une salle occupée par des personnes.
Dans un lieu clos, la concentration en CO2 de l’air augmente vite lorsque des personnes sont présentes, chaque adulte rejetant, par sa respiration, environ 18 litres par heure de ce gaz à pression atmosphérique. Mais l’ouverture des fenêtres permet de revenir très rapidement à une concentration normale. C’est ce qu’illustre ce graphique, issu des mesures par l’un des auteurs (Jean-Michel Courty) de la teneur en CO2 dans son bureau, au fil de ses allées et venues et des ouvertures et fermetures de la fenêtre. Crédit : © J.-M. Courty/Pour la Science.
En conclusion
En mesurant le taux de CO2 dans une salle de classe, ou n’importe quelle pièce où on réunit plusieurs personnes pendant un certain temps, on peut utiliser les formules dont on a parlé pour se fixer des objectifs permettant une dilution qui assurera la limitation des risques de transmission du virus.
Espérons que cette analyse vous permettra d’ajouter l’aération à votre arsenal de gestes barrière.
Point de vigilance : le contenu de cette page ne montre en aucun cas que la distance physique ne sert à rien, encore moins que les masques sont inutiles. Bien au contraire !
Concernant les mesures de CO2, vous pouvez notamment consulter le site projetCO2.fr ou Le site du collectif Nous aérons qui donnent des conseils sur comment procéder, quels capteurs utiliser, etc.
Vous y trouverez un ensemble d'informations très utiles en complément de la modélisation qui vient de vous être exposée.
Sitographie
|→ Le contenu de cette page est une libre retranscription de la vidéo intitulée « Comment limiter la transmission aérienne du COVID ? », d'une durée de 22 minutes 6 secondes, publiée le 30 avril 2021, écrite et réalisée par David Louapre © Science étonnante, hébergée sur la chaîne YouTube ScienceEtonnante - Que son auteur en soit très chaleureusement remercié pour sa libre utilisation.


